ResNet相关的一些介绍及代码复现
ResNet学习笔记及仿真
前言
深度残差网络(Deep Residual Network)是cnn机器视觉史上的一件里程碑的事件,在2015年,ResNet在ImageNet和COCO数据集上获得了非常优秀的成绩。如下所示:
- ImageNet Classification: “Ultra-deep”
152-layernets - ImageNet Detection:
16%better than 2nd - ImageNet Localization:
27%better than 2nd - COCO Detection:
11%better than 2nd - COCO Segmentation:
12%better than 2nd
ResNet获得了五项第一,再一次的刷新了CNN模型在ImageNet上的历史[1],而论文的作者何凯明也获得了CVPR2016最佳论文奖[2]。以下是记录了解ResNet的一些笔记,主要是来自于15年和16年何凯明所在的微软研究院发表的论文。
深度网络退化问题(degradation problem of deep network)
从AlexNet到GoogLeNet,看起来好像是网络越深越好,但是直接秉持着We need go deeper的思想构建神经网络,到最后会发现,随着网络越来越深,会出现梯度消失(vanishing gradients)和梯度爆炸(exploding gradients)以及网络退化(network degradation):
- 梯度消失和爆炸(vanishing/exploding gradients):网络层数太深引发的梯度方向传播中的连乘效应引起
- 网络退化(network degradation):较深的模型可以看作是较浅模型的超空间,理论上较深的模型可以看作是较浅模型的恒等映射,但是实际上较深模型后面添加的不是恒等映射,而是一些非线性层[3]
对于梯度消失和爆炸的应对方法如下:
- 改换激活函数: 使用
relu、LeakyRelu、ELU等激活函数可以改善梯度消散或爆炸问题。relu导数的正数部分恒等于1,所以不会产生梯度消失和梯度爆炸 - BatchNormalization: 对每一层的输入做scale和shift方法,将每层神经元的输入分布强行拉回均值为0、方差为1的标准正态分布,这就使得激活层输入值落入在非线性函数对输入值比较敏感的区域,使得输入的小变化会导致损失函数较大的变化,使得梯度变大,训练速度加快,且避免梯度消失问题
- 梯度剪切: 该方法主要是针对梯度爆炸提出。其思想是设置一个梯度剪切阈值,更新梯度时,如果梯度超过这个阈值,那么限制其在这个范围之内
但是随着网络的加深,可以看到的是训练误差和测试误差都开始增加,这自然不是过拟合引起的,而是网络出现退化[4],如figure1所示:
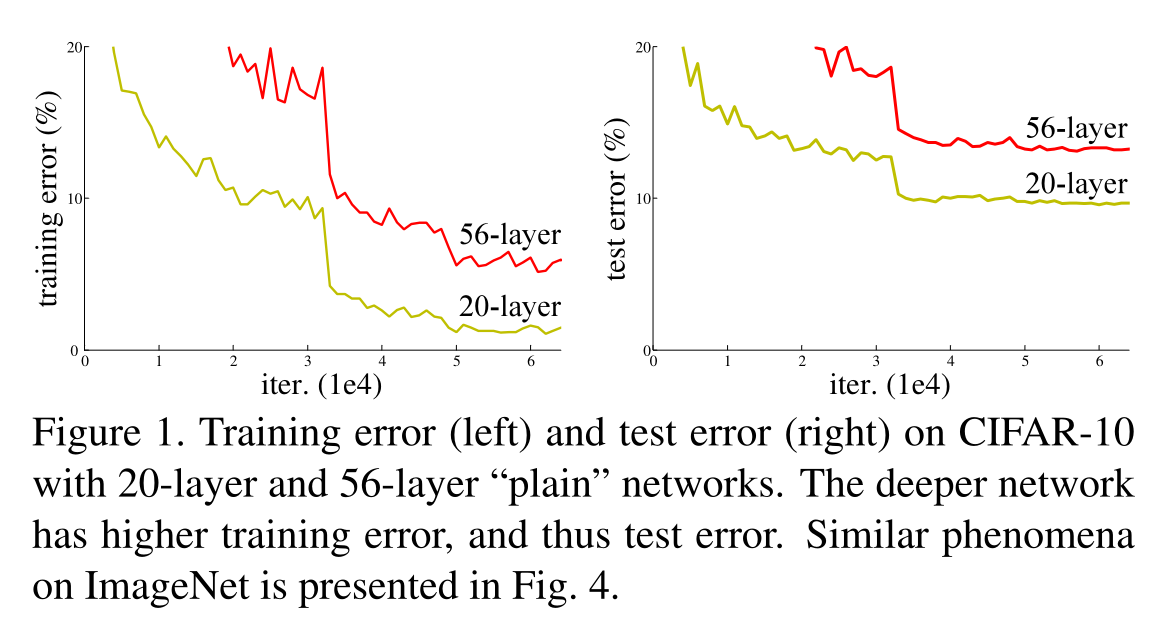
网络退化表明了并非所有系统都同样容易优化。考虑一个较深的网络和一个较浅的网络,更深的网络对应更浅的网络相当于是增加了更多的层,添加的层可以是恒等映射(identity mapping),而其他的层是相当于是更浅的模型中直接复制的,这种构造容易得到,较深的模型不会产生比较浅的模型更高的训练误差,但是实验表明,简单地加深网络模型会出现网络退化的问题。
残差块(Residual block)
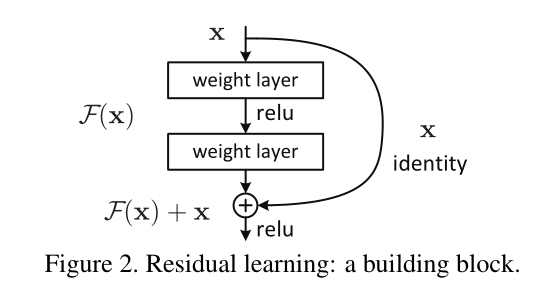
网络退化出现的原因就是现有的网络无法实现恒等映射,将想要得到的恒等映射函数表示为 $H(x)=x$,残差块网络设计为 $H(x)=F(x)+x$,即直接将恒等映射作为网络的一部分,就可以将问题转化为学习一个残差函数 $F(x)=H(x)-x$,那么只要 $F(x)=0$,就可以构成一个恒等映射 $H(x)=x$,拟合残差比拟合恒等映射容易的多[5]。从数学上更加详细地描述残差结构,可以是:
$$
y=F(x, W_i)+x
$$
其中 $x$ 和 $y$ 表示的分别是所考虑的层的输入和输出向量,函数 $F(x, W_i)$ 表示要学习的残差映射,操作 $F(x, W_i)+x$ 是通过跳接实现,在方程1中 $x$ 和 $F$ 的维度必须相同,否则,需要对跳接进行线性投影 $W_s$ 来匹配维度:
$$
y=F(x, W_i)+W_s x
$$
$F(x)+x$ 的公式可以通过具有跳接(shortcut connections)的前馈神经网络来实现,跳接可以是跳过一层或者多层的连接,通过跳接在激活函数前,将上一层或几层的输出与本层输出相加,将求和结果输入到激活函数作为本层的输出,残差块示例如figure2所示
跳接只是执行恒等映射,他们的输出被添加到堆叠层的输出中,这不会增加额外的参数,也不会增加计算复杂性
添加了残差网络,可以给神经网络一个多的选择,例如学习到的一层的参数是冗余的,那么就可以直接走跳接路线,跳过这个冗余层,而不用去拟合参数使得输出 $H(x)=x$
学习残差的计算量比学习输出等于输入小:例如普通网络为A,残差网络为B,输入为2,输出为2,那么普通网络就是$A(2)=2$,而残差网络就是$B(2)=F(2)+2=2$,即残差网络中$F(2)=0$。一般网络会将权重初始化为0附近的数,所以让$F(2)$拟合0会比$A(2)=2$容易
ReLU能够将负数激活为0,正数等于输出,这相当于过滤了负数的线性变化,让$F(x)=0$变的更加容易
对残差网络$H(x)=F(x)+x$求梯度,即反向传播时,得到$H’(x)=F’(x)+1$,残差结构的这个常数1能够保证求梯度的时候梯度不会消失
这种结构不仅适用于全连接层,还适用于卷积层,逐通道地对两个特征图执行元素相加
网络架构
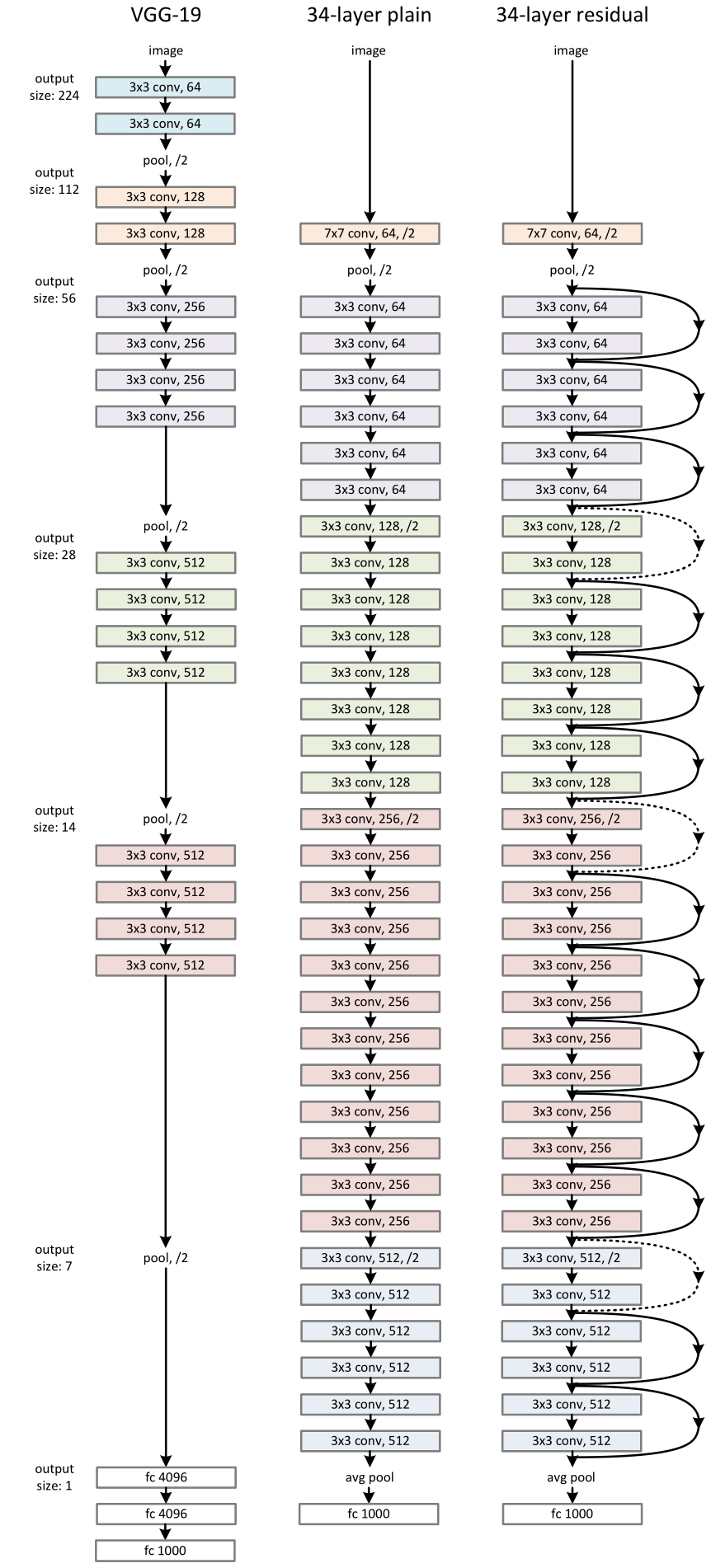
网络结构如figure3所示,从左到右分别是VGG-19(196亿次浮点运算)、34层不带残差的plain net(36亿次浮点运算)、34层的残差网络(36亿次浮点运算)
plain network
- 主要受到VGGNet的启发,遵循两个简单设计规则:
- 对于相同的输出特征图大小,层具有相同数量的滤波器
- 如果特征图大小减半,则过滤器的数量加倍
- 步长为2的卷积层直接执行下采样
- 网络结尾是一个整体平均池化层和一个1000路的全连接层和softmax函数
- 总体的带权重的层是34层
- 该模型比VGGNet相比具有更少的滤波器和更低的复杂度,plain net 有36亿次浮点运算,而VGG-19有196亿次浮点运算,前者是后者的18%
Residual Network
- 在plain net网络中引入了跳接(shortcut conncetions),将其转换为了对应的残差版本
- 跳接引入有两种形式:
实现细节
- 遵循AlexNet数据预处理的方法,对图像进行裁剪和水平翻转得到224 x 224的图像,然后减去每个像素的平均值[6]
- 每次卷积之后和激活函数之前采用批处理标准化(batch normalization, BN)
- 批大小(mini-batch )为256
- 学习率(learning rate) 从 0.1 开始,当误差平稳时,学习率除以10,模型训练了 $60 \times 10^4$ 次迭代
- 权重衰减(weight decay)0.0001,动量(momentum)为 0.9
- 网络中没有使用到dropout
实验结果
ImageNet分类结果
对比了18层和34层的plain net以及对应的ResNet,可以看到如figure4所示,残差结果确实解决了退化问题
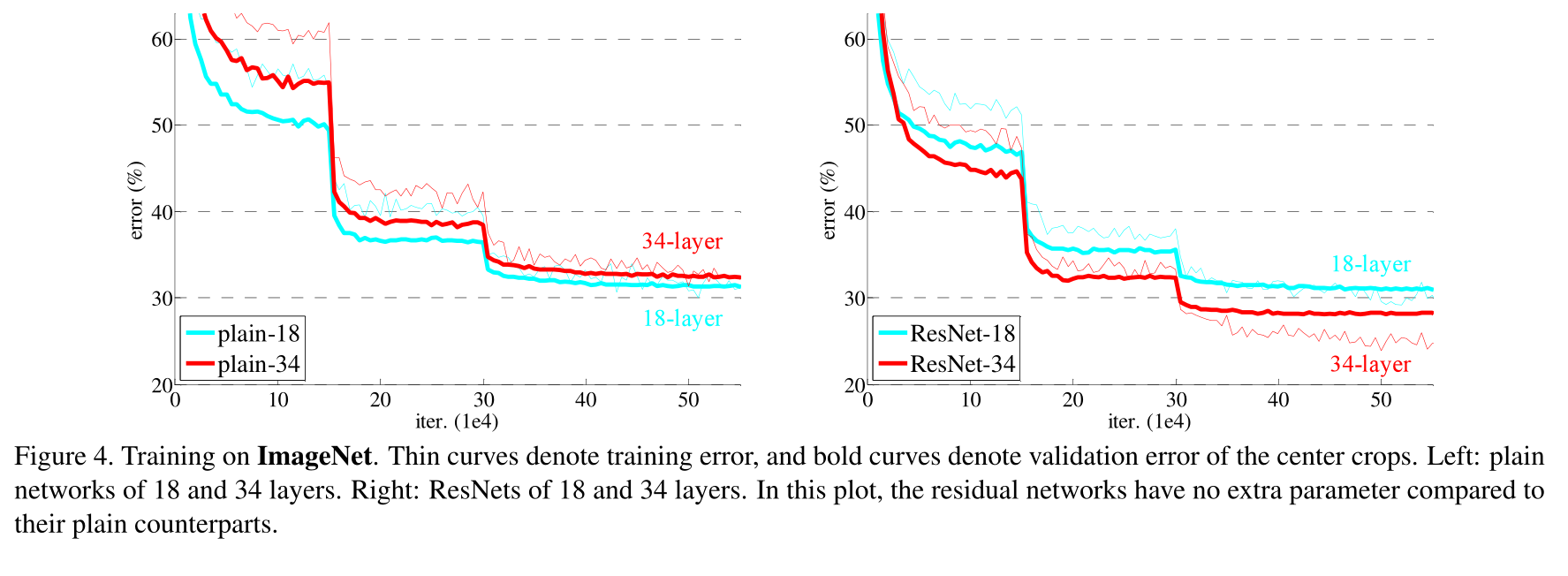
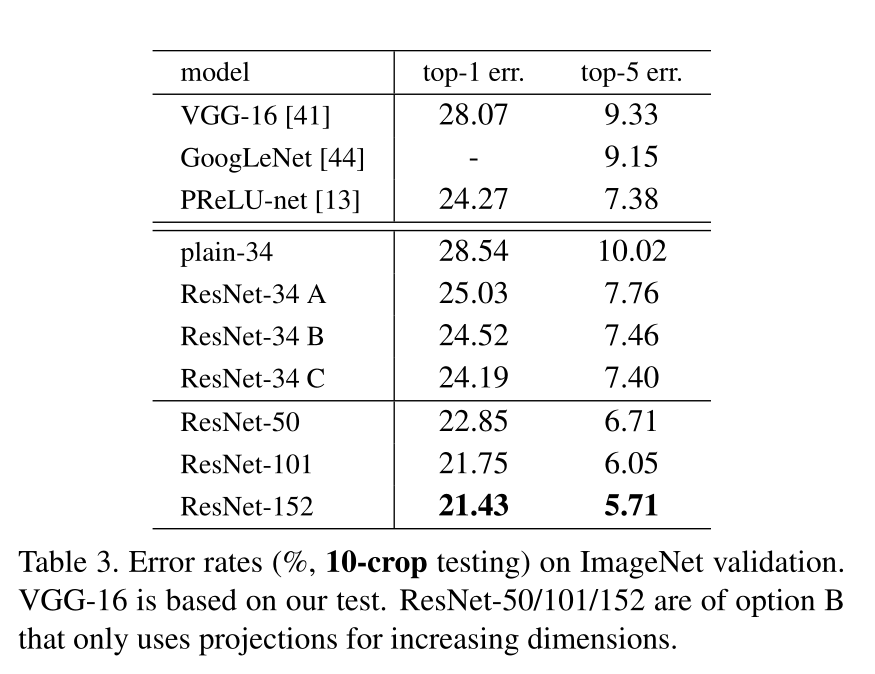
对比了ImageNet数据集的测试结果汇总如表3所示
基于cifar10数据集的ResNet实现[7]
导入基本模块
1 | |
torchvision下载cifar10数据集
1 | |
1 | |
Using downloaded and verified file: ../data\cifar-10-python.tar.gz
Extracting ../data\cifar-10-python.tar.gz to ../data
Files already downloaded and verified
1 | |

1 | |
'cuda'
BasicBlock

1 | |
1 | |
BasicBlock(
(features): Sequential(
(0): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential(
(0): Conv2d(64, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
torch.Size([2, 128, 32, 32])
Bottleneck Block
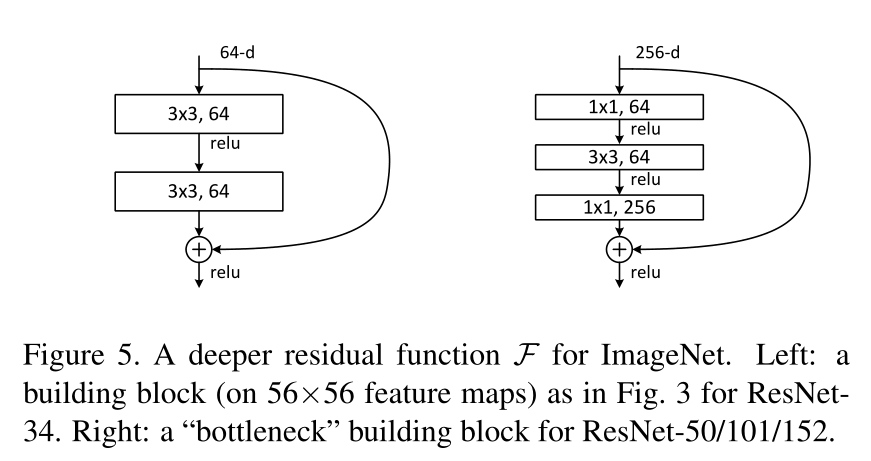
1 | |
1 | |
Bottleneck(
(features): Sequential(
(0): Conv2d(256, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(5): ReLU(inplace=True)
(6): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(7): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential(
(0): Conv2d(256, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
torch.Size([2, 512, 32, 32])
ResNet

1 | |
1 | |
1 | |
ResNet(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
)
(layer1): Sequential(
(0): BasicBlock(
(features): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(1): BasicBlock(
(features): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(2): BasicBlock(
(features): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
)
(layer2): Sequential(
(0): BasicBlock(
(features): Sequential(
(0): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential(
(0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(features): Sequential(
(0): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(2): BasicBlock(
(features): Sequential(
(0): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(3): BasicBlock(
(features): Sequential(
(0): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
)
(layer3): Sequential(
(0): BasicBlock(
(features): Sequential(
(0): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential(
(0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(features): Sequential(
(0): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(2): BasicBlock(
(features): Sequential(
(0): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(3): BasicBlock(
(features): Sequential(
(0): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(4): BasicBlock(
(features): Sequential(
(0): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(5): BasicBlock(
(features): Sequential(
(0): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
)
(layer4): Sequential(
(0): BasicBlock(
(features): Sequential(
(0): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential(
(0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(features): Sequential(
(0): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
(2): BasicBlock(
(features): Sequential(
(0): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace=True)
(3): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(4): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(shortcut): Sequential()
)
)
(avg_pool): AvgPool2d(kernel_size=4, stride=4, padding=0)
(classifer): Linear(in_features=512, out_features=10, bias=True)
)
1 | |
torch.Size([2, 10])
train model
1 | |
1 | |
1 | |
start_epoch: 0
1 | |
Epoch: 0
[1, 100] loss: 118.672118 | Acc: 56.953% (7290/12800)
[1, 200] loss: 235.403772 | Acc: 57.355% (14683/25600)
[1, 300] loss: 342.972803 | Acc: 58.721% (22549/38400)
Total loss: 436.702453
Epoch: 1
[2, 100] loss: 95.490529 | Acc: 65.930% (8439/12800)
[2, 200] loss: 189.245391 | Acc: 66.246% (16959/25600)
[2, 300] loss: 279.333860 | Acc: 66.758% (25635/38400)
Total loss: 357.071455
Epoch: 2
[3, 100] loss: 76.589579 | Acc: 73.203% (9370/12800)
[3, 200] loss: 151.513288 | Acc: 73.492% (18814/25600)
[3, 300] loss: 224.068864 | Acc: 73.836% (28353/38400)
Total loss: 286.139592
Epoch: 3
[4, 100] loss: 62.455524 | Acc: 78.664% (10069/12800)
[4, 200] loss: 125.946750 | Acc: 78.246% (20031/25600)
[4, 300] loss: 186.423765 | Acc: 78.414% (30111/38400)
Total loss: 240.281207
Epoch: 4
[5, 100] loss: 54.547970 | Acc: 81.414% (10421/12800)
[5, 200] loss: 110.654127 | Acc: 80.898% (20710/25600)
[5, 300] loss: 166.249208 | Acc: 80.919% (31073/38400)
Total loss: 215.950420
Epoch: 5
[6, 100] loss: 48.104260 | Acc: 83.109% (10638/12800)
[6, 200] loss: 99.401246 | Acc: 82.734% (21180/25600)
[6, 300] loss: 148.791911 | Acc: 82.807% (31798/38400)
Total loss: 194.453984
Epoch: 6
[7, 100] loss: 44.256123 | Acc: 85.352% (10925/12800)
[7, 200] loss: 90.796863 | Acc: 84.582% (21653/25600)
[7, 300] loss: 138.052944 | Acc: 84.396% (32408/38400)
Total loss: 181.198413
Epoch: 7
[8, 100] loss: 40.750996 | Acc: 85.906% (10996/12800)
[8, 200] loss: 84.440442 | Acc: 85.539% (21898/25600)
[8, 300] loss: 127.751372 | Acc: 85.430% (32805/38400)
Total loss: 168.756287
Epoch: 8
[9, 100] loss: 40.119882 | Acc: 86.266% (11042/12800)
[9, 200] loss: 79.863018 | Acc: 86.211% (22070/25600)
[9, 300] loss: 120.620995 | Acc: 86.188% (33096/38400)
Total loss: 158.876436
Epoch: 9
[10, 100] loss: 35.623312 | Acc: 87.477% (11197/12800)
[10, 200] loss: 75.740778 | Acc: 86.777% (22215/25600)
[10, 300] loss: 115.162053 | Acc: 86.703% (33294/38400)
Total loss: 151.007361
Epoch: 10
[11, 100] loss: 34.881428 | Acc: 88.039% (11269/12800)
[11, 200] loss: 71.926582 | Acc: 87.699% (22451/25600)
[11, 300] loss: 109.965547 | Acc: 87.375% (33552/38400)
Total loss: 145.488317
Epoch: 11
[12, 100] loss: 32.708189 | Acc: 88.977% (11389/12800)
[12, 200] loss: 66.790455 | Acc: 88.594% (22680/25600)
[12, 300] loss: 103.832237 | Acc: 88.125% (33840/38400)
Total loss: 137.913376
Epoch: 12
[13, 100] loss: 31.950675 | Acc: 89.242% (11423/12800)
[13, 200] loss: 65.730325 | Acc: 88.820% (22738/25600)
[13, 300] loss: 101.885522 | Acc: 88.430% (33957/38400)
Total loss: 135.173613
Epoch: 13
[14, 100] loss: 29.611200 | Acc: 89.805% (11495/12800)
[14, 200] loss: 62.823584 | Acc: 89.129% (22817/25600)
[14, 300] loss: 97.116191 | Acc: 88.849% (34118/38400)
Total loss: 129.670478
Epoch: 14
[15, 100] loss: 29.925015 | Acc: 89.875% (11504/12800)
[15, 200] loss: 62.226747 | Acc: 89.516% (22916/25600)
[15, 300] loss: 95.177161 | Acc: 89.206% (34255/38400)
Total loss: 126.196716
Epoch: 15
[16, 100] loss: 28.724815 | Acc: 90.039% (11525/12800)
[16, 200] loss: 60.983424 | Acc: 89.551% (22925/25600)
[16, 300] loss: 93.304751 | Acc: 89.354% (34312/38400)
Total loss: 123.906554
Epoch: 16
[17, 100] loss: 27.764434 | Acc: 90.305% (11559/12800)
[17, 200] loss: 57.115116 | Acc: 90.148% (23078/25600)
[17, 300] loss: 89.535789 | Acc: 89.685% (34439/38400)
Total loss: 118.733271
Epoch: 17
[18, 100] loss: 26.901688 | Acc: 90.781% (11620/12800)
[18, 200] loss: 56.244663 | Acc: 90.316% (23121/25600)
[18, 300] loss: 87.834935 | Acc: 89.872% (34511/38400)
Total loss: 116.597480
Epoch: 18
[19, 100] loss: 27.289408 | Acc: 90.633% (11601/12800)
[19, 200] loss: 57.436502 | Acc: 90.137% (23075/25600)
[19, 300] loss: 88.500381 | Acc: 89.846% (34501/38400)
Total loss: 115.314192
Epoch: 19
[20, 100] loss: 24.068543 | Acc: 91.852% (11757/12800)
[20, 200] loss: 53.208921 | Acc: 90.828% (23252/25600)
[20, 300] loss: 84.727040 | Acc: 90.203% (34638/38400)
Total loss: 112.072869
Epoch 21: reducing learning rate of group 0 to 1.0000e-02.
Epoch: 20
[21, 100] loss: 17.140250 | Acc: 94.570% (12105/12800)
[21, 200] loss: 30.638147 | Acc: 95.156% (24360/25600)
[21, 300] loss: 41.904663 | Acc: 95.573% (36700/38400)
Total loss: 51.213734
Epoch: 21
[22, 100] loss: 7.424102 | Acc: 97.984% (12542/12800)
[22, 200] loss: 14.609958 | Acc: 97.918% (25067/25600)
[22, 300] loss: 21.400117 | Acc: 97.964% (37618/38400)
Total loss: 27.305064
Epoch: 22
[23, 100] loss: 5.123270 | Acc: 98.586% (12619/12800)
[23, 200] loss: 9.734514 | Acc: 98.684% (25263/25600)
[23, 300] loss: 14.615595 | Acc: 98.648% (37881/38400)
Total loss: 19.189702
Epoch: 23
[24, 100] loss: 3.460799 | Acc: 99.172% (12694/12800)
[24, 200] loss: 6.807557 | Acc: 99.203% (25396/25600)
[24, 300] loss: 10.049018 | Acc: 99.211% (38097/38400)
Total loss: 13.315432
Epoch: 24
[25, 100] loss: 2.478284 | Acc: 99.469% (12732/12800)
[25, 200] loss: 4.640014 | Acc: 99.492% (25470/25600)
[25, 300] loss: 6.763096 | Acc: 99.505% (38210/38400)
Total loss: 9.023635
Epoch: 25
[26, 100] loss: 1.528404 | Acc: 99.680% (12759/12800)
[26, 200] loss: 2.968595 | Acc: 99.711% (25526/25600)
[26, 300] loss: 4.535004 | Acc: 99.706% (38287/38400)
Total loss: 5.932488
Epoch: 26
[27, 100] loss: 1.165903 | Acc: 99.852% (12781/12800)
[27, 200] loss: 2.107836 | Acc: 99.867% (25566/25600)
[27, 300] loss: 3.091869 | Acc: 99.875% (38352/38400)
Total loss: 4.153865
Epoch: 27
[28, 100] loss: 0.732892 | Acc: 99.945% (12793/12800)
[28, 200] loss: 1.651403 | Acc: 99.883% (25570/25600)
[28, 300] loss: 2.452116 | Acc: 99.888% (38357/38400)
Total loss: 3.153302
Epoch: 28
[29, 100] loss: 0.618112 | Acc: 99.945% (12793/12800)
[29, 200] loss: 1.297444 | Acc: 99.941% (25585/25600)
[29, 300] loss: 1.891233 | Acc: 99.943% (38378/38400)
Total loss: 2.471666
Epoch: 29
[30, 100] loss: 0.548403 | Acc: 99.945% (12793/12800)
[30, 200] loss: 1.019150 | Acc: 99.953% (25588/25600)
[30, 300] loss: 1.501457 | Acc: 99.958% (38384/38400)
Total loss: 1.972135
Epoch: 30
[31, 100] loss: 0.435647 | Acc: 99.969% (12796/12800)
[31, 200] loss: 0.805838 | Acc: 99.977% (25594/25600)
[31, 300] loss: 1.260185 | Acc: 99.971% (38389/38400)
Total loss: 1.586358
Epoch: 31
[32, 100] loss: 0.347193 | Acc: 99.992% (12799/12800)
[32, 200] loss: 0.633916 | Acc: 99.992% (25598/25600)
[32, 300] loss: 0.942637 | Acc: 99.995% (38398/38400)
Total loss: 1.342172
Epoch: 32
[33, 100] loss: 0.301421 | Acc: 99.984% (12798/12800)
[33, 200] loss: 0.628001 | Acc: 99.980% (25595/25600)
[33, 300] loss: 0.972346 | Acc: 99.982% (38393/38400)
Total loss: 1.273002
Epoch: 33
[34, 100] loss: 0.271426 | Acc: 100.000% (12800/12800)
[34, 200] loss: 0.522611 | Acc: 100.000% (25600/25600)
[34, 300] loss: 0.791412 | Acc: 99.997% (38399/38400)
Total loss: 1.069014
Epoch: 34
[35, 100] loss: 0.272007 | Acc: 100.000% (12800/12800)
[35, 200] loss: 0.500229 | Acc: 100.000% (25600/25600)
[35, 300] loss: 0.741914 | Acc: 99.997% (38399/38400)
Total loss: 0.962418
Epoch: 35
[36, 100] loss: 0.200861 | Acc: 100.000% (12800/12800)
[36, 200] loss: 0.421179 | Acc: 100.000% (25600/25600)
[36, 300] loss: 0.637626 | Acc: 100.000% (38400/38400)
Total loss: 0.835531
Epoch: 36
[37, 100] loss: 0.200766 | Acc: 100.000% (12800/12800)
[37, 200] loss: 0.397603 | Acc: 100.000% (25600/25600)
[37, 300] loss: 0.606028 | Acc: 99.995% (38398/38400)
Total loss: 0.800073
Epoch: 37
[38, 100] loss: 0.178643 | Acc: 100.000% (12800/12800)
[38, 200] loss: 0.374064 | Acc: 100.000% (25600/25600)
[38, 300] loss: 0.577130 | Acc: 100.000% (38400/38400)
Total loss: 0.768444
Epoch: 38
[39, 100] loss: 0.192881 | Acc: 100.000% (12800/12800)
[39, 200] loss: 0.412415 | Acc: 99.996% (25599/25600)
[39, 300] loss: 0.607835 | Acc: 99.997% (38399/38400)
Total loss: 0.769075
Epoch: 39
[40, 100] loss: 0.174156 | Acc: 100.000% (12800/12800)
[40, 200] loss: 0.356172 | Acc: 100.000% (25600/25600)
[40, 300] loss: 0.544260 | Acc: 100.000% (38400/38400)
Total loss: 0.711841
Epoch: 40
[41, 100] loss: 0.197980 | Acc: 99.992% (12799/12800)
[41, 200] loss: 0.405721 | Acc: 99.996% (25599/25600)
[41, 300] loss: 0.596260 | Acc: 99.997% (38399/38400)
Total loss: 0.783890
Epoch: 41
[42, 100] loss: 0.195553 | Acc: 99.992% (12799/12800)
[42, 200] loss: 0.377932 | Acc: 99.996% (25599/25600)
[42, 300] loss: 0.565132 | Acc: 99.997% (38399/38400)
Total loss: 0.740863
Epoch: 42
[43, 100] loss: 0.184922 | Acc: 100.000% (12800/12800)
[43, 200] loss: 0.370228 | Acc: 99.996% (25599/25600)
[43, 300] loss: 0.563876 | Acc: 99.997% (38399/38400)
Total loss: 0.738950
Epoch: 43
[44, 100] loss: 0.188086 | Acc: 100.000% (12800/12800)
[44, 200] loss: 0.363090 | Acc: 100.000% (25600/25600)
[44, 300] loss: 0.529876 | Acc: 100.000% (38400/38400)
Total loss: 0.684271
Epoch 45: reducing learning rate of group 0 to 1.0000e-03.
Epoch: 44
[45, 100] loss: 0.180676 | Acc: 99.992% (12799/12800)
[45, 200] loss: 0.349191 | Acc: 99.996% (25599/25600)
[45, 300] loss: 0.512983 | Acc: 99.997% (38399/38400)
Total loss: 0.664923
Epoch: 45
[46, 100] loss: 0.166781 | Acc: 100.000% (12800/12800)
[46, 200] loss: 0.320780 | Acc: 100.000% (25600/25600)
[46, 300] loss: 0.477024 | Acc: 100.000% (38400/38400)
Total loss: 0.632136
Epoch: 46
[47, 100] loss: 0.153178 | Acc: 100.000% (12800/12800)
[47, 200] loss: 0.315739 | Acc: 100.000% (25600/25600)
[47, 300] loss: 0.473674 | Acc: 100.000% (38400/38400)
Total loss: 0.619973
Epoch: 47
[48, 100] loss: 0.163760 | Acc: 100.000% (12800/12800)
[48, 200] loss: 0.322436 | Acc: 100.000% (25600/25600)
[48, 300] loss: 0.487261 | Acc: 100.000% (38400/38400)
Total loss: 0.619886
Epoch: 48
[49, 100] loss: 0.160341 | Acc: 100.000% (12800/12800)
[49, 200] loss: 0.328375 | Acc: 100.000% (25600/25600)
[49, 300] loss: 0.497179 | Acc: 100.000% (38400/38400)
Total loss: 0.643087
Epoch: 49
[50, 100] loss: 0.156791 | Acc: 100.000% (12800/12800)
[50, 200] loss: 0.309782 | Acc: 100.000% (25600/25600)
[50, 300] loss: 0.466129 | Acc: 100.000% (38400/38400)
Total loss: 0.606150
Epoch 51: reducing learning rate of group 0 to 1.0000e-04.
save model
1 | |
evaluate
1 | |

1 | |
参考文献
- [2] 何凯明个人主页