深度优先遍历二叉树
655.输出二叉树
难度中等198收藏分享切换为英文接收动态反馈
给你一棵二叉树的根节点 root ,请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ,用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则:
- 树的 高度 为
height,矩阵的行数m应该等于height + 1。 - 矩阵的列数
n应该等于2height+1 - 1。 - 根节点 需要放置在 顶行 的 正中间 ,对应位置为
res[0][(n-1)/2]。 - 对于放置在矩阵中的每个节点,设对应位置为
res[r][c],将其左子节点放置在res[r+1][c-2height-r-1],右子节点放置在res[r+1][c+2height-r-1]。 - 继续这一过程,直到树中的所有节点都妥善放置。
- 任意空单元格都应该包含空字符串
""。
返回构造得到的矩阵 res 。
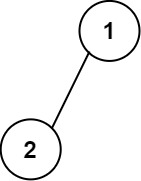
示例 1:
1 | |
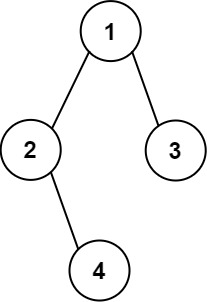
示例 2:
1 | |
提示:
- 树中节点数在范围
[1, 210]内 -99 <= Node.val <= 99- 树的深度在范围
[1, 10]内
题解
直接通过深度优先遍历获取树的高度,然后创建一个(m, n)的二维字符串list,之后递归的遍历树,并将对应结点的值放在该二维字符串list数组中
1 | |
- 时间复杂度:
- 空间复杂度:
655.输出二叉树
http://example.com/2022/08/23/leetcode每日一题/655.输出二叉树/