782.变为棋盘

难度困难156收藏分享切换为英文接收动态反馈

一个 n x n 的二维网络 board 仅由 0 和 1 组成 。每次移动，你能任意交换两列或是两行的位置。

返回 将这个矩阵变为 “棋盘” 所需的最小移动次数 。如果不存在可行的变换，输出 -1。

“棋盘” 是指任意一格的上下左右四个方向的值均与本身不同的矩阵。

示例 1:

输入: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
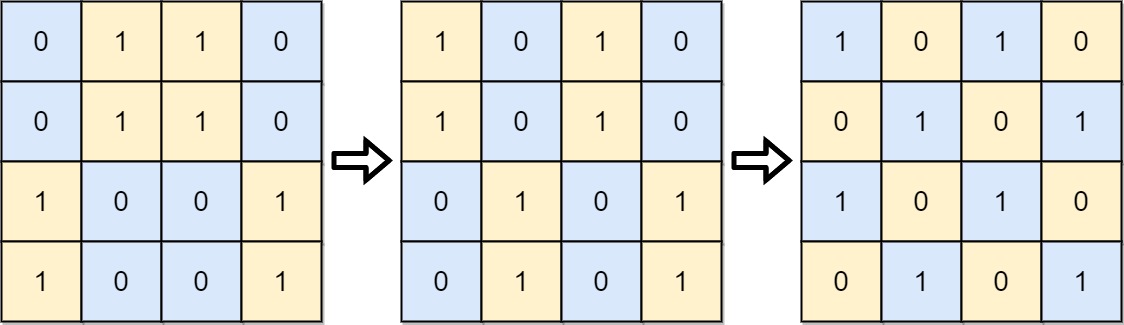
输出: 2
解释:一种可行的变换方式如下，从左到右：
第一次移动交换了第一列和第二列。
第二次移动交换了第二行和第三行。

示例 2:

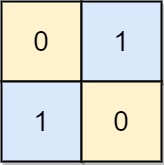
输入: board = [[0, 1], [1, 0]]
输出: 0
解释: 注意左上角的格值为0时也是合法的棋盘，也是合法的棋盘.

示例 3:

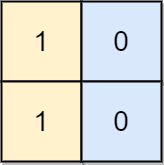
输入: board = [[1, 0], [1, 0]]
输出: -1
解释: 任意的变换都不能使这个输入变为合法的棋盘。

提示：

• n == board.length
• n == board[i].length
• 2 <= n <= 30
• board[i][j] 将只包含 0或 1

题解

完全不会

class Solution {
    int n = 0, INF = 0x3f3f3f3f;
    int getCnt(int a, int b) {
        return Integer.bitCount(a) != Integer.bitCount(b) ? INF : Integer.bitCount(a ^ b) / 2;
    }
    public int movesToChessboard(int[][] g) {
        n = g.length;
        int r1 = -1, r2 = -1, c1 = -1, c2 = -1, mask = (1 << n) - 1;
        for (int i = 0; i < n; i++) {
            int a = 0, b = 0;
            for (int j = 0; j < n; j++) {
                if (g[i][j] == 1) a += (1 << j);
                if (g[j][i] == 1) b += (1 << j);
            }
            if (r1 == -1) r1 = a;
            else if (r2 == -1 && a != r1) r2 = a;
            if (c1 == -1) c1 = b;
            else if (c2 == -1 && b != c1) c2 = b;
            if (a != r1 && a != r2) return -1;
            if (b != c1 && b != c2) return -1;
        }
        if (Integer.bitCount(r1) + Integer.bitCount(r2) != n) return -1;
        if (Integer.bitCount(c1) + Integer.bitCount(c2) != n) return -1;
        if ((r1 ^ r2) != mask || (c1 ^ c2) != mask) return -1;
        int t = 0;
        for (int i = 0; i < n; i += 2) t += (1 << i);
        int ans = Math.min(getCnt(r1, t), getCnt(r2, t)) + Math.min(getCnt(c1, t), getCnt(c2, t));
        return ans >= INF ? -1 : ans;
    }
}