面试手撕代码总结

LeetCode突击面试刷题

基础题

19. 删除链表的倒数第 N 个结点

难度中等2229

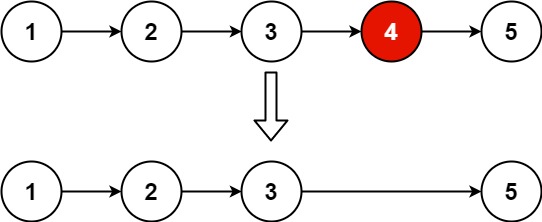
给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

img

1
2
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

1
2
输入：head = [1], n = 1
输出：[]

示例 3：

1
2
输入：head = [1,2], n = 1
输出：[1]

提示：

  • 链表中结点的数目为 sz
  • 1 <= sz <= 30
  • 0 <= Node.val <= 100
  • 1 <= n <= sz

进阶：你能尝试使用一趟扫描实现吗？

题解

首先设置一个指针cur，先往后走n步

再设置一个指针pre，初始化为head

两个指针cur和pre同时向后移动，直到cur.next==null，这时候pre指向的就是倒数第k个结点的前驱，直接删除即可

注意一个特殊情况：n等于链表长度的时候，就是删除第一个结点，直接返回

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode cur = head;
        while(n-- > 0 && cur.next != null) {
            cur = cur.next;
        }
        // 删除最后一个节点
        if (cur.next == null && n == 0)
            return head.next;
        
        // 找到删除节点的前驱结点
        ListNode pre = head;
        while(cur.next != null) {
            cur = cur.next;
            pre = pre.next;
        }

        // 删除第k个结点
        pre.next = pre.next.next;
        return head;  
    }
}

image-20220923182024626

643. 子数组最大平均数 I

难度简单266

给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。

请你找出平均数最大且 长度为 k 的连续子数组，并输出该最大平均数。

任何误差小于 10-5 的答案都将被视为正确答案。

示例 1：

1
2
3
输入：nums = [1,12,-5,-6,50,3], k = 4
输出：12.75
解释：最大平均数 (12-5-6+50)/4 = 51/4 = 12.75

示例 2：

1
2
输入：nums = [5], k = 1
输出：5.00000

提示：

  • n == nums.length
  • 1 <= k <= n <= 105
  • -104 <= nums[i] <= 104

题解

前缀和+滑动窗口

首先计算一下前缀和，然后利用滑动窗口计算对应区间的子数组和，并统计其中最大的区间和，最后输出与k的商

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public double findMaxAverage(int[] nums, int k) {
        int ans = Integer.MIN_VALUE;
        int n = nums.length;
        int[] sum = new int[n+1];
        for (int i = 0; i < n; i++) {
            sum[i+1] = sum[i] + nums[i];
        }

        for (int i = 0; i < n; i++) {
            int right = i + k;
            if (right < n + 1) {
                int temp = sum[right] - sum[i];
                ans = Math.max(ans, temp);
            }
        }
        return ans * 1.0 / k;
    }
}

image-20220923203827589

直接滑动窗口

直接通过滑动窗口计算滑动窗口中子数组的和，每次移动的时候减去上一个窗口左边界的值，加上下一个窗口右边界的值，记录其中窗口中的最大和，然后返回最大平均值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution {
    public double findMaxAverage(int[] nums, int k) {
        int ans = Integer.MIN_VALUE;
        int n = nums.length;
        int sum = 0;
        for (int i = 0; i < k; i++) {
            sum += nums[i];
        }

        int left = 0, right = k - 1;
        while (right < n) {
            ans = Math.max(ans, sum);
            sum -= nums[left++];
            if (right >= n - 1)
                break;
            sum += nums[++right];

        }
        return ans * 1.0 / k;
    }
}

image-20220923204823308

贪心

253. 会议室 II

难度中等474收藏分享切换为英文接收动态反馈

给你一个会议时间安排的数组 intervals ，每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ，返回 所需会议室的最小数量 。

示例 1：

1
2
输入：intervals = [[0,30],[5,10],[15,20]]
输出：2

示例 2：

1
2
输入：intervals = [[7,10],[2,4]]
输出：1

提示：

  • 1 <= intervals.length <= 104
  • 0 <= starti < endi <= 106

通过次数56,832

提交次数109,355

题解

考虑先将会议按照开始时间排序，需要多少会议室可以转换为同一时间在进行的最多有多少会议

  • 使用优先队列记录每个会议室的最晚结束的会议的结束时间
  • 新来的会议如果开始时间比现有最早结束会议的结束时间早，那么就会存在冲突，必须开辟新的会议，并将这个新的会议的结束时间添加到优先队列
  • 否则，则跳过，不用添加新的会议室
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int minMeetingRooms(int[][] intervals) {
        Arrays.sort(intervals, (a, b)->a[0] - b[0]);
        PriorityQueue<Integer> pq = new PriorityQueue<>();
        int ans = 0;
        for (int i = 0; i < intervals.length; i++) {
            pq.offer(intervals[i][1]);
            if (intervals[i][0] < pq.peek()) {
                ans++;
            } else {
                pq.poll();
            }
        }
        return ans;
    }
}

image-20220923125740865

1057. 校园自行车分配

难度中等92收藏分享切换为英文接收动态反馈

在 X-Y 平面上表示的校园中，有 n 名工人和 m 辆自行车，其中 n <= m。

给定一个长度为 n 的数组 workers ，其中 worker [i] = [xi, yi] 表示第 i 个工人的位置。你也得到一个长度为 m 的自行车数组 bikers ，其中 bikes[j] = [xj, yj] 是第 j 辆自行车的位置。所有给定的位置都是 唯一 的。

我们需要为每位工人分配一辆自行车。在所有可用的自行车和工人中，我们选取彼此之间 曼哈顿距离 最短的工人自行车对 (workeri, bikej) ，并将其中的自行车分配給工人。

如果有多个 (workeri, bikej) 对之间的 曼哈顿距离 相同，那么我们选择 工人索引最小 的那对。类似地，如果有多种不同的分配方法，则选择 自行车索引最小 的一对。不断重复这一过程，直到所有工人都分配到自行车为止。

返回长度为 n 的向量 answer，其中 answer[i] 是第 i 位工人分配到的自行车的索引（从 0 开始）。

给定两点 p1 和 p2 之间的 曼哈顿距离 为 Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|。

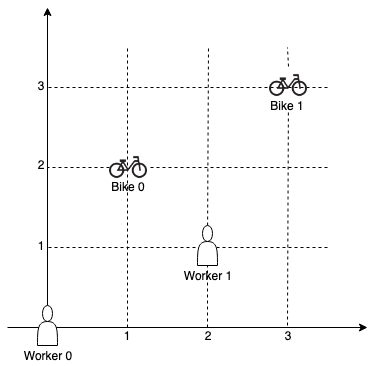
示例 1：

img

1
2
3
输入：workers = [[0,0],[2,1]], bikes = [[1,2],[3,3]]
输出：[1,0]
解释：工人 1 分配到自行车 0，因为他们最接近且不存在冲突，工人 0 分配到自行车 1 。所以输出是 [1,0]。

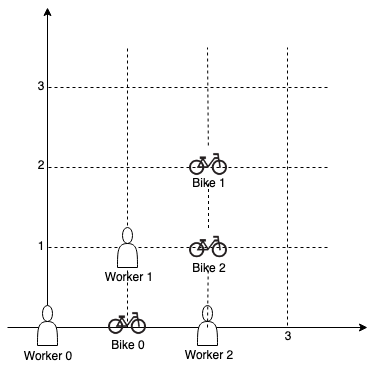
示例 2：

img

1
2
3
输入：workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
输出：[0,2,1]
解释：工人 0 首先分配到自行车 0 。工人 1 和工人 2 与自行车 2 距离相同，因此工人 1 分配到自行车 2，工人 2 将分配到自行车 1 。因此输出为 [0,2,1]。

提示：

  • n == workers.length
  • m == bikes.length
  • 1 <= n <= m <= 1000
  • workers[i].length == bikes[j].length == 2
  • 0 <= xi, yi < 1000
  • 0 <= xj, yj < 1000
  • 所有工人和自行车的位置都不相同

题解

可以直接将worker编号和bike编号以及距离distance组成三元组放在优先队列中，然后根据题目意思设置优先队列排序条件

然后遍历优先队列，获取分配情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
    public int[] assignBikes(int[][] workers, int[][] bikes) {
        int[] ans = new int[workers.length];

        PriorityQueue<Pair> pq = new PriorityQueue<>((a, b)->{
            if (a.distance != b.distance)
                return a.distance - b.distance;
            else if (a.worker != b.worker)
                return a.worker - b.worker;
            else
                return a.bike - b.bike;
        });

        for (int i = 0; i < workers.length; i++) {
            for (int j = 0; j < bikes.length; j++) {
                int distance = manhattenDistance(workers[i], bikes[j]);
                Pair pair = new Pair(i, j, distance);
                pq.offer(pair);
            }
        }

        boolean[] workered = new boolean[workers.length];
        boolean[] biked = new boolean[bikes.length];

        while (pq.size() > 0) {
            Pair pair = pq.poll();
            if (!workered[pair.worker] && !biked[pair.bike]) {
                ans[pair.worker] = pair.bike;
                workered[pair.worker] = true;
                biked[pair.bike] = true;
            }
        }

        return ans;
    }

    public int manhattenDistance(int[] worker, int[] bike) {
        return Math.abs(worker[0] - bike[0]) + Math.abs(worker[1] - bike[1]);
    }
}

class Pair{
    int worker, bike, distance;
    Pair(int worker, int bike, int distance) {
        this.worker = worker;
        this.bike = bike;
        this.distance = distance;
    }
}

image-20220923133857564

678. 有效的括号字符串

难度中等525收藏分享切换为英文接收动态反馈

给定一个只包含三种字符的字符串：（ ，） 和 *，写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则：

  1. 任何左括号 ( 必须有相应的右括号 )。
  2. 任何右括号 ) 必须有相应的左括号 ( 。
  3. 左括号 ( 必须在对应的右括号之前 )。
  4. * 可以被视为单个右括号 ) ，或单个左括号 ( ，或一个空字符串。
  5. 一个空字符串也被视为有效字符串。

示例 1:

1
2
输入: "()"
输出: True

示例 2:

1
2
输入: "(*)"
输出: True

示例 3:

1
2
输入: "(*))"
输出: True

注意:

  1. 字符串大小将在 [1，100] 范围内。

题解

可以定义左括号的数量上限为l，下限为r，遍历字符串，可能出现三种情况：

  • 当前字符为(，l++, r++
  • 当前字符为)，l--, r--
  • 当前字符为*，l--, r++

在判断过程中可能出现l<0，重置为0，遍历过程中如果出现l>r，那么括号不合法，直接返回false

最后返回l==0的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean checkValidString(String s) {
        int l = 0, r = 0;
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                l++; r++;
            } else if (s.charAt(i) == ')') {
                l--; r--;
            } else {
                l--; r++;
            }
            l = Math.max(0, l);
            if (l > r) return false;
        }
        return l==0;
    }
}

image-20220923145218066

动态规划

647. 回文子串

难度中等981

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

1
2
3
输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

1
2
3
输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

提示：

  • 1 <= s.length <= 1000
  • s 由小写英文字母组成

题解

定义 $dp[l][r]$ 表示字符串从l到r这一段是否为回文，可以得到只要dp[l+1][r-1]=true且s[l]=s[r]即可以说dp[l][r]为回文

初始情况：l=r时，dp[l][r] = true

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int countSubstrings(String s) {
        if (s.length() < 2)
            return 1;
        int n = s.length(), ans = 0;
        boolean[][] dp = new boolean[n][n];
        char[] chars = s.toCharArray();

        for (int r = 0; r < n; r++) {
            for (int l = 0; l <= r; l++) {
                if (chars[l] == chars[r] && (r - l <= 2 || dp[l+1][r-1])) {
                    dp[l][r] = true;
                    ans++;
                }
            }
        }
        return ans;
    }
}

image-20220925215546662

5. 最长回文子串

难度中等5751

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

1
2
3
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

1
2
输入：s = "cbbd"
输出："bb"

提示：

  • 1 <= s.length <= 1000
  • s 仅由数字和英文字母组成

题解

同上一道题类似，需要注意一些边界问题的不同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public String longestPalindrome(String s) {
        if (s.length() < 2)
            return s;

        int n = s.length();
        char[] chars = s.toCharArray();
        boolean[][] dp = new boolean[n][n];

        int maxLen = 1;
        int start = 0;

        for (int r = 1; r < n; r++) {
            for (int l = 0; l < r; l++) {
                if (chars[l] == chars[r] && (r - l <= 2 || dp[l + 1][r - 1])) {
                    dp[l][r] = true;
                    if (r - l + 1 > maxLen) {
                        maxLen = r - l + 1;
                        start = l;
                    }
                }
            }
        }
        return s.substring(start, start + maxLen);
    }
}

image-20220925214257338

64. 最小路径和

难度中等1355

给定一个包含非负整数的 *m* x *n* 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

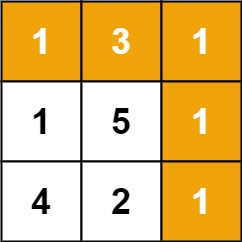
示例 1：

img

1
2
3
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

1
2
输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 200
  • 0 <= grid[i][j] <= 100

题解

设置dp[i][j]表示到grid[i][j]的最短路径，可以得到动态转移方程
$$
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
$$
注意初始化左上角的网格已经走过的路径为0，为了保证处理过程的问题，初始化dp为Integer.MAX_VALUE，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int minPathSum(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int ans = Integer.MAX_VALUE;
        int[][] dp = new int[n + 1][m + 1];
        for (int i = 0; i <= n; i++)
            Arrays.fill(dp[i], Integer.MAX_VALUE);
        dp[0][0] = 0;
        dp[0][1] = 0;
        dp[1][0] = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i-1][j-1];
            }
        }
        return dp[n][m];
    }
}

image-20220925224803941

递归回溯

46. 全排列

难度中等2228

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

1
2
输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

1
2
输入：nums = [1]
输出：[[1]]

提示：

  • 1 <= nums.length <= 6
  • -10 <= nums[i] <= 10
  • nums 中的所有整数 互不相同

题解

递归回溯法解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    List<List<Integer>> ans;
    public List<List<Integer>> permute(int[] nums) {
        int n = nums.length;
        ans = new ArrayList<List<Integer>>();
        if (n == 0)
            return ans;
        dfs(0, n, new ArrayList<Integer>(), nums, new boolean[n]);
        return ans;
    }

    public void dfs(int cnt, int n, List<Integer> path, int[] nums, boolean[] visited) {
        if (cnt == n) {
            ans.add(new ArrayList<Integer>(path));
            return ;
        }

        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                path.add(nums[i]);
                visited[i] = true;
                dfs(cnt + 1, n, path, nums, visited);
                path.remove(path.size() - 1);
                visited[i] = false;
            }
        }
    }
}

image-20220923192716279

47. 全排列 II

难度中等1196

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

1
2
3
4
5
输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

题解

这道题和全排列的思想类似，需要处理的一点就是去除重复的一点

可以添加一个判断条件

if (i > 0 && nums[i] == num[i-1] && !visited[i-1])

这一个判断条件可以保证相邻元素的填入顺序是

  • [未填入，未填入，未填入]
  • [填入，未填入，未填入]
  • [填入，填入，未填入]
  • [填入，填入，填入]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public class Solution {
    List<List<Integer>> ans;
    public List<List<Integer>> permuteUnique(int[] nums) {
        int n = nums.length;
        ans = new ArrayList<List<Integer>>();
        Arrays.sort(nums);
        if (n == 0)
            return ans;
        dfs(0, n, new ArrayList<Integer>(), nums, new boolean[n]);
        return ans;
    }

    public void dfs(int cnt, int n, List<Integer> path, int[] nums, boolean[] visited) {
        if (cnt == n) {
            ans.add(new ArrayList<Integer>(path));
            return ;
        }

        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                // 去除重复
                if (i > 0 && nums[i] == nums[i - 1] && !visited[i-1])
                    continue;
                path.add(nums[i]);
                visited[i] = true;
                dfs(cnt + 1, n, path, nums, visited);
                path.remove(path.size() - 1);
                visited[i] = false;
            }
        }
    }
    
}

image-20220923201356717

面试
#Java #offer #后端开发 #八股文 #面试
面试突击刷题笔记
http://example.com/2022/09/25/面试记录/面试突击刷题笔记/
作者
madao33
发布于
September 25, 2022
许可协议